为什么麦当劳和肯德基总是开在一起?

你一定发现过这样的规律:如果有两家商店卖同一个品类的东西,又互为竞争对手,那么它们一定开在一起——众所周知,每个肯德基的附近一定有一家麦当劳,每个某两字房产中介的旁边一定是某四字中介,哪怕像奶茶店咖啡店这种并不是只有两个品牌突出的行业,往往也是好几家同类的店铺挤在一起。小区门口的超市和理发店更是同理。

对于消费者来说,最方便的布局应该是各种店铺均匀分布在一条街上,这样无论买什么东西,走的距离都是最短的。然而现实却是要么一整条街都没有店铺,只要有一定是各个竞争对手挤在一起。这是为什么?
要理解商家为什么这样选择,就要从商家的角度思考问题。我们假设小区门口有一条东西向的街道,某商家甲发现了在这卖早餐的商机,于是率先占据了街上最中心的位置,以便吸引从各个方向过来的顾客。商家乙看到了甲生意兴隆,决定效仿加入。面对抢生意的乙,甲除了接受也别无他法。最终双方协商,甲在西半条街的中点,乙在东半条街的中点,甲乙各占整条街的 50%,形成一种平衡。
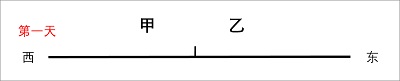
然而真实的商战往往朴实无华。第二天,商家乙趁甲不在,越过分界线,向西移动了 20 米,分走了整条街 60% 的顾客,来晚的甲只能捡漏剩下的 40%;甲也不甘示弱,隔天又去了乙的东边,拦下来东边那 60% 的客源;从此甲乙两方不断变换位置,试图多分走对方一部分客流量,而最终的结果是两人在整条街的中点达成平衡。只有在这个平衡点的位置,双方才能维持各自现有的最高收益。在博弈论中,这一现象被称为纳什均衡。
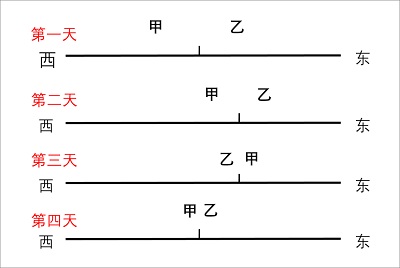
所以,在选址上,同类店铺不会平均分布,而是集中在一起,或者挤在一个街角。虽然从顾客的视角看,店铺集中起来意味着买东西要走更远的路,但对于商家来说,只有这样做才能在竞争中实现互相制衡,让自己的利益最大化。因此,纳什均衡并不能实现「社会最优解」。
纳什均衡的突破性在于它打破了传统经济学中只考虑经营成本的思维方式,而是涵盖了竞争对手的想法,以及双方博弈的过程如何影响自己。对于被卷入竞争的店铺来说,这个思路下做出的决策不一定是对自己最有利的,却是基于纳什均衡的前提下对自己最合适的策略。

博弈论中的霍特林法则,描述的也是这一规律:卖相似产品的店铺,因为竞争,最终都会开到一起;同理,在一个理性市场中,对于两个竞争者最好的方案就是做得越来越像。
此外,多个竞争者开在同一条街上,就会构成一个小型商圈,把原本分散的消费者集中起来,聚合人气,形成规模,最终形成的也是一种共赢。

